1. Regression(회귀)/Classification(분류) 문제 해결을 위한 솔루션
- KNN
- Logistic Regression
- LDA
- Decision Tree
- SVM
- Ensemble
- Kmeans
2. 판별 분석(Discriminant Analysis)
(1) 정의
두 개 이상의 모 집단에서 추출된 표본들이 지니고 있는 정보를 이용하여, 이 표본들이 어느 모집단에서 추출된 것인지는 결정해 줄 수 있는 기준을 찾는 분석법

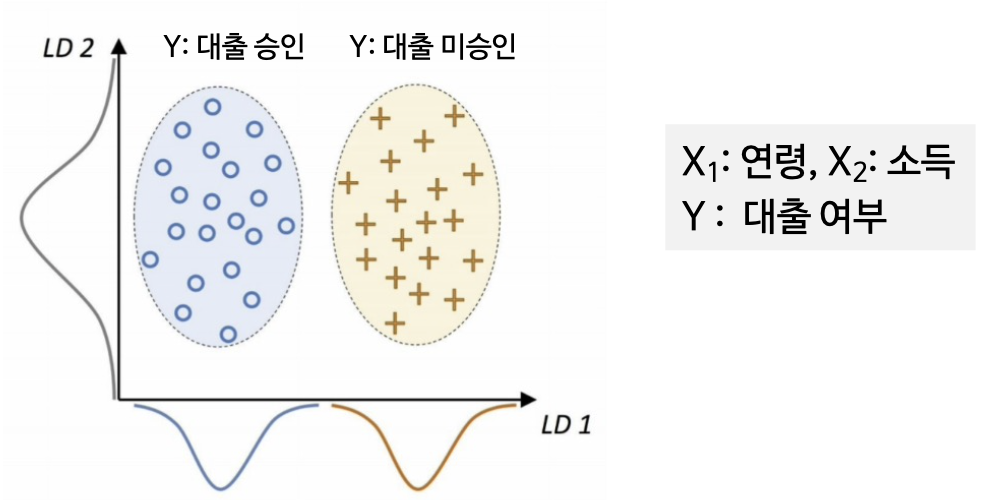
예) 은행에서 부동산 담보 대출을 행하고자 할 경우, 채무자가 대출금을 갚을 것인가?
과거 대출금을 반환치 않은 사람의 정보 유형(연령,소득,결혼 유무등)을 참고하여 담보 신청 시 신청자의 정보 유형을 과거의 유형과 비교하여 장래 변제 가능성을 파악할 수 있음 (*학습 기반 분류 방법의 핵심)
(2) 개념
판별 변수(Discriminant variable)
판별변수는 어떤 집단에 속하는지 판별하기 위한 변수로서 독립변수 중 판별력이 높은 변수를 뜻한다. 판별변수를 선택하는데 판별 기여도 외에 고려해야 할 사항은 다른 독립변수들과의 상관관계이며, 상관관계가 높은 두 독립변수를 선택하는 것보다는 두 독립변수 중 하나를 판별 변수로 선택하고, 그것과 상관관계가 적은 독립변수를 선택함으로써 효과적인 판별 함수를 만들 수 있다.
판별 함수(Discriminant function)
판별분석이 이용되기 위해서는 각 개체는 여러 집단 중에서 어느 집단에 속해있는지 알려져 있어야 하며(supervised learning) 소속 집단이 이미 알려진 경우에 대하여 변수들(x)을 측정하고, 이들 변수들을 이용하여 각 집단을 가장 잘 구분해낼 수 있는 판별식을 만들어 분별하는 과정을 포함하게 된다.
판별 점수 (Discriminant score)
어떤 대상이 어떤 집단에 속하는지 판별하기 위하여 그 대상의 판별변수들의 값을 판별함수에 대입하여 구한 값
표본의 크기
전체 표본의 크기는 통상적으로 독립변수의 개수보다 3배(최소 2배) 이상 되어야 한다. 종속변수의 집단 각각의 표본의 크기 중 최소 크기가 독립변수의 개수보다 커야한다(판별력을 좌우하는 것이 전체 표본의 수가 아니라 가장 적은 집단의 표본의 수이기 때문).
(3) 단계
1) 케이스가 속한 집단을 구분하는 데 기여할 수 있는 독립 변수 찾기
2) 집단을 구분하는 기준이 되는 독립 변수들의 선형 결합인 판별 함수 도출
3) 도출된 판별 함수에 의해 (train data) 분류의 정확도를 분석
4) 판별 함수를 이용하여 새로운 케이스(test data)가 속하는 클래스 예측
독립 변수 ← Feature Engineering
판별 함수 ← 다양한 기계학습 방법론을 통해 학습하는 대상
판별 점수의 집단간 변동과 집단내 변동의 배율을 최대화하는 판별 함수를 도출

3. 선형 판별 분석(LDA)
(1) 가정 (Assumptions)
각 클래스 집단은 정규분포(normal distribution) 형태의 확률분포를 가지고, 비슷한 형태의 공분산(covariance, 2개의 확률변수의 상관 정도를 나타내는 값) 구조를 가짐
(2) LDA는 판별과 차원축소의 기능
2차원(두 가지 독립변수)의 두가지 범주(주황, 파랑)를 갖는 데이터를 분류하는 문제에서 LDA는 먼저 하나의 차원(1d)에 projection을 하여 차원을 축소시킨다.
- LDA는 차원 축소의 개념을 포함
- 2차원 자료들을 판별 축에 정사영시킨 분포의 형태를 고려
(3) LDA의 결정 경계(decision boundary)의 특징
Projection 축(실선)에 직교하는 축(점선)으로, 정사영(projection)은 두 분포의 특징이 아래의 목표를 달성해야 한다.
- 각 클래스 집단의 평균의 차이가 큰 지점을 결정 경계로 지정
- 각 클래스 집단의 분산이 작은 지점을 결정 경계로 지정
- 분산 대비 평균의 차이를 극대화하는 결정 경계를 찾고자 하는 것으로, 사영 데이터의 분포에서 겹치는 영역이 작은 결정 경계를 선택

(4) 요약
결정 경계
- 분산 대비 평균의 차이를 극대화하는 경계
가정
- 각 클래스 집단은 정규분포(normal distribution) 형태의 확률분포를 가짐
- 각 클래스 집단은 비슷한 형태의 공분산(covariance) 구조를 가짐
장점
- 변수 간(x) 공분산 구조를 반영
공분산 구조 가정이 살짝 위반되더라도, 비교적 robust하게 동작함
단점
- 가장 작은 그룹의 샘플수가 설명변수의 개수보다 많아야 함
- 정규분포 가정에 크게 벗어나는 경우 잘 동작하지 못함
- 범주 사이(y)에 공분산 구조가 많이 다른 경우를 반영하지 못함 → 이차판별분석법(QDA)를 통해 해결 가능
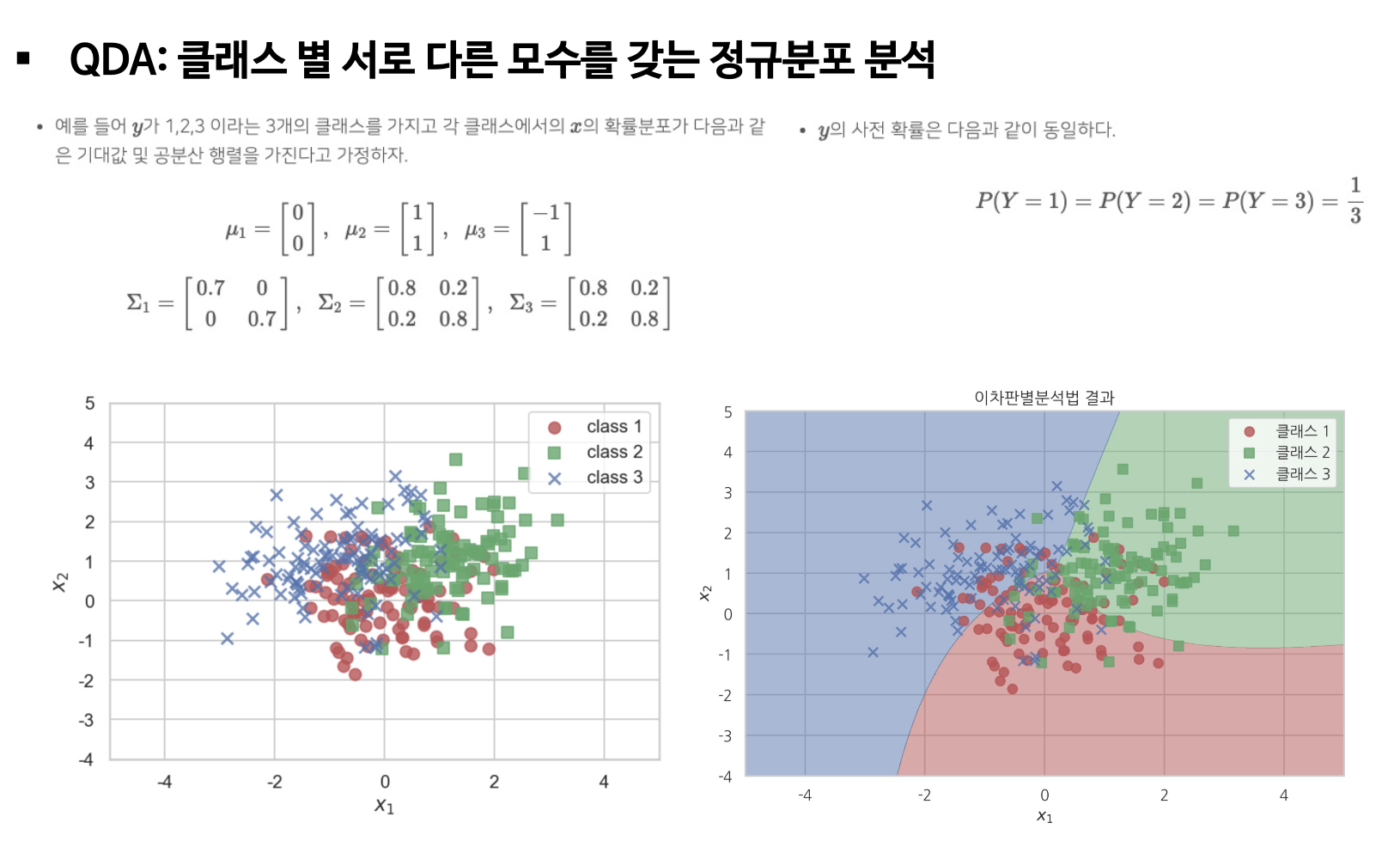
4. 이차 판별 분석(QDA)
(1) 정의
K(범주의 수)와 관계없이 공통 공분산 구조에 대한 가정을 만족하지 못하면 QDA 적용 (Y의 범주 별로 서로 다른 공분산 구조를 가진 경우에 활용 가능)
(2) LDA와 QDA 비교
- (첫번째 그림) LDA 결정 경계는 선형으로 가정하고 있어 서로 다른 공분산 분류에 어려움이 있음
- (두번째 그림) LDA도 같은 공분산의 비선형 분류 가능 → 변수의 제곱을 한 추가적인 변수들을 통해 보완
- (세번째 그림) QDA는 서로 다른 공분산 데이터 분류 가능 → 비선형 분류 가능
- QDA는 서로 다른 공분산 데이터 분류를 위해 샘플이 많이 필요 → 설명변수의 개수가 많을수록, 추정해야 하는 모수가 많아짐 (연산량 큼)

(3) 예시
'Computer Science > Machine Learning' 카테고리의 다른 글
| Discriminant analysis(판별 분석) [Discriminant Analysis 이용 원자력발전소 상태 예측] (3) (0) | 2024.03.31 |
|---|---|
| Discriminant analysis(판별 분석) [Iris] (2) (0) | 2024.03.31 |
| Linear Regression : Logistic Regression [수면시간에 따른 우울증 예측] (6) (0) | 2024.03.24 |
| Linear Regression : Logistic Regression [은하계 종류 예측] (5) (0) | 2024.03.24 |
| Linear Regression : Logistic Regression [Wine] (4) (0) | 2024.03.24 |


