4. VGGNet
VGGNet은 2014년 옥스퍼드 대학교의 VGG 연구 그룹에서 제안한 신경망 구조
VGGNet의 구성 요소는 새로 고안된 요소 없이 LeNet이나 AlexNet과 동일하지만 신경망의 층수가 더 많음
VGG16 이라고 알려진 VGGNet은 가중치를 가진 층 16개로 구성 (합성곱층 13개, 전결합층 3개)
모든 층의 하이퍼파라미터가 동일하게 설정되었기 때문에 신경망을 이해하기 쉽다는 점이 학계에 깊은 인상을 남김
(1) VGGNet에서 발전된 부분
VGGNet의 개선점은 동일하게 설정된 층(합성곱층과 전결합층)을 사용해서 신경망 구조를 단순화 시켰다는 점임
전체적인 신경망 구조는 일련의 합성곱층 뒤에 역시 풀링층이 배치되는 구조로 모든 합성곱층은 3x3 크기의 필터와 스트라이드 1, 패딩 1이 적용되었고, 모든 풀링층은 2x2크기의 풀링 영역과 스트라이드 2가 적용되었음
VGGNet에서 합성곱층의 필터 크기를 줄인(3x3) 이유는 AlexNet(11x11, 5x5)보다 더 세밀한 특징을 추출하기 위해서임
수용영역의 크기가 같을 때 크기가 큰 하나의 커널보다 크기가 작은 커널을 여러 개 쌓은쪽이 더 성능이 좋음
→ 커널을 여러 개 쌓으며 비선형층을 늘리는 것이 신경망의 층수를 늘리는 것과 동일한 효과가 있기 때문
→ 파라미터 수를 억제하므로 더 낮은 비용으로 더 복잡한 특징을 학습할 수 있음
커널을 여러 개 쌓으며 비선형층을 늘리는 것이 신경망의 층수를 늘리는 것과 동일
- 커널의 크기가 3x3인 합성곱층을 두 층 쌓은 구조(합성곱층 사이에 풀링층은 두지 않음)는 5x5 크기의 수용 영역을 가진 합성곱층과 효과가 동등함
- 커널의 크기가 3x3인 합성곱층을 세 층 쌓은 구조(합성곱층 사이에 풀링층은 두지 않음)는 7x7 크기의 수용 영역을 가진 합성곱층과 효과가 동등함
- 따라서 수용영역 크기가 3x3인 커널을 여러 개 쌓으면 비선형함수 ReLU를 여러 개 포함시키는 것과 같아 결정 함수의 변별력을 향상시키는 효과가 있음
파라미터 수를 억제하는 효과
- C개 채널을 가진 7x7 크기의 커널을 가진 단일 합성곱층의 파라미터 수는 $7^2 C^2 = 49 C^2$
- 3x3 크기의 커널을 3개 쌓은 구조의 파라미터수는 $3*3^2 C^2 = 27 C^2$개로 절반 가까이로 억제하는 효과가 있음
VGGNet은 이렇게 합성곱 연산과 풀링 연산이 일어나는 구조를 통합하는 방법으로 전체 신경망의 구조를 단순하게 유지해서 신경망에 대한 이해 및 구현 편의성을 개선함
VGGNet은 3x3 크기의 커널을 여러 층 쌓은 합성곱층 사이에 간간이 2x2 크기의 풀링 연산을 하는 풀링층을 끼워 넣는 식으로 구성됨
이 구조 뒤에 다시 일반적인 전결합층과 소프트맥스 함수가 배치되는 전형적인 분류기 구조가 배치됨
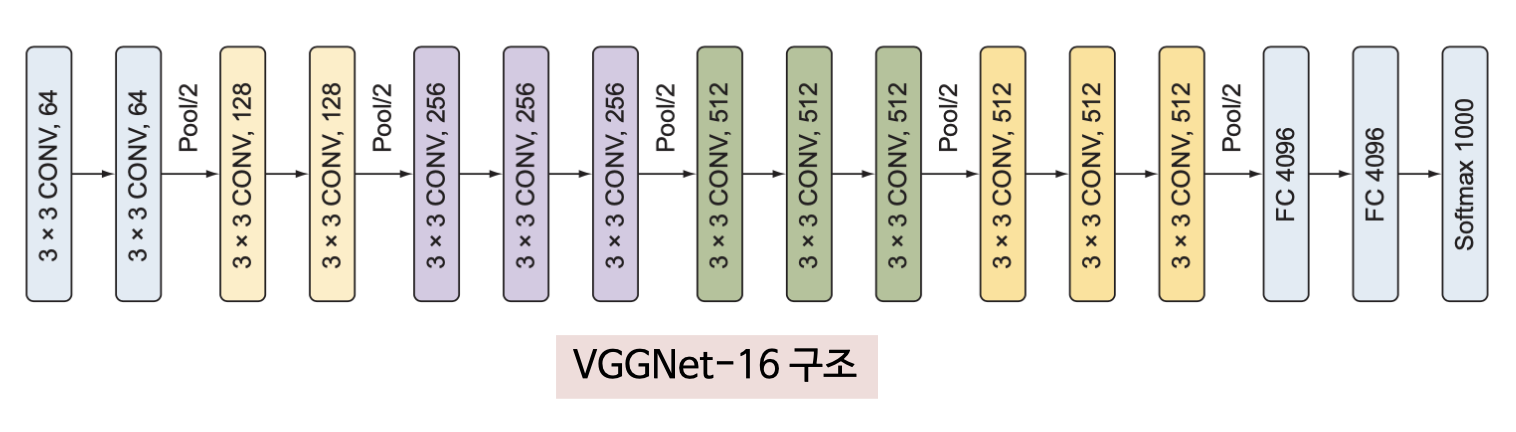
수용영역 (receptive field)
수용영역은 출력의 한 점에 영향을 미치는 입력 이미지의 범위를 의미
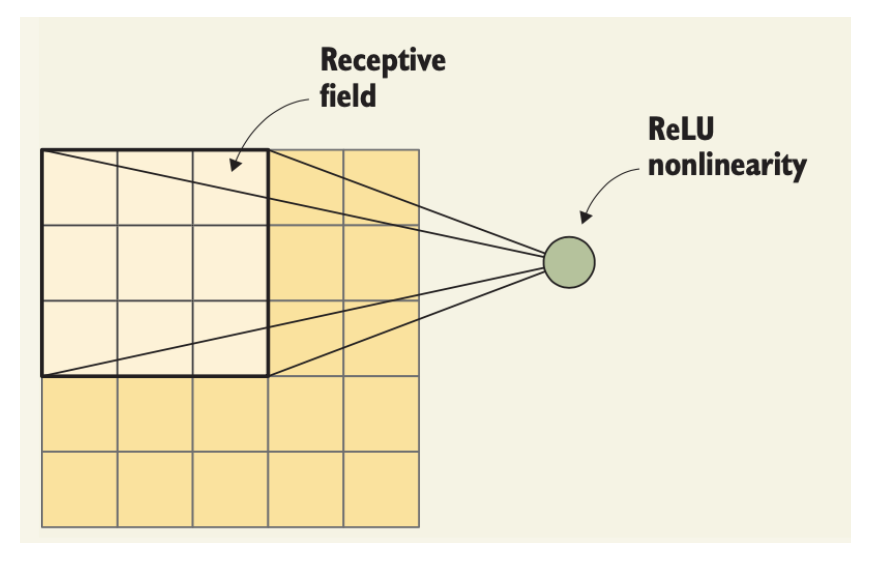
(2) VGGNet의 다양한 버전
구성 D와 E가 가장 일반적으로 사용되며 가중치를 포함하는 층수를 붙여 이들을 각각 VGG16, VGG19라고 부름
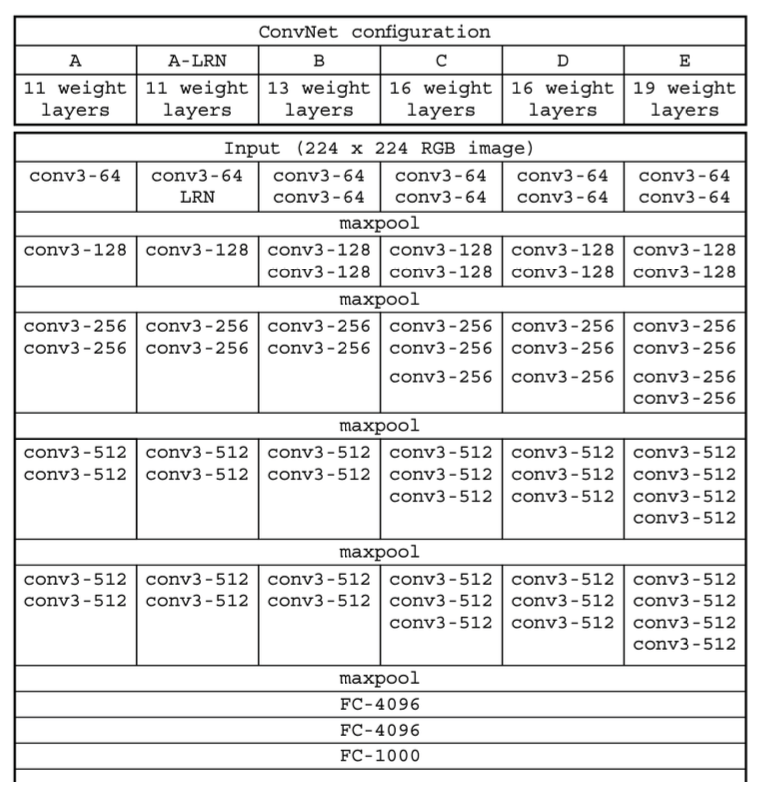
VGG16은 약 1억 3800만개의 파라미터가 있으며, VGG19의 파라미터 수는 약 1억 4400만 개
VGG16이 VGG19보다 더 적은 파라미터로 거의 동등한 성능을 내기 때문에 일반적으로는 VGG16이 더 널리 쓰임

VGGNet 중 VGG16과 VGG19가 층수가 많은 만큼 더 복잡한 모델을 학습할 수 있어 구현에 자주 사용됨
VGGNet 논문에서는 과적합을 방지하기 위해 사용한 규제화 기법
- 가중치 감쇠율 5x10-4 을 적용한 L2 규제화
- 편의를위해아래구현코드에는포함하지않았음
- 비율이 0.5인 드롭아웃을 마지막 층을 제외한 두 전결합충에 적용했음
(3) 하이퍼파라미터 설정
VGGNet의 학습 과정은 AlexNet의 학습 과정을 많이 참고했음
미니배치 경사 하강법을 사용하되 모멘텀 0.9를 적용했음
학습률은 초깃값 0.01로 시작해서 검증 데이터의 정확도가 정체될 때 마다 1/10 로 감소시킴
(4) VGGNet의 성능
VGG16의 이미지넷 데이터셋에 대한 Top-5오차는 8.1%로, 15.3%의 오차를 기록했던 AlexNet에 비해 개선된 성능을 보였음
VGG19의 성능은 이보다 더 높은 7.4%를 기록함
AlexNet보다 층수가 많고 파라미터 수가 더 많음에도 VGGNet 의 파라미터가 더욱 빨리 수렴했다는 것은 층수를 늘리고 합성곱 필터의 크기를 줄이면서 규제화와 같은 효과가 발생했기 때문임
5. 인셉션과 GoogLeNet
인셉션은 구글에서 연구 논문을 통해 2014년에 발표했음
인셉션의 구조의 특징은 신경망 내부적으로 계산 자원의 효율을 높였음
인셉션 신경망 구조를 구현한 GoogLeNet은 22개 층으로 구성(VGGNet보다 층수가 많음)되었으나 파라미터 수는 VGGNet의 1/12에 불가함
→ VGGNet: 1억 3800만개, GoogLeNet: 1300만개
GoogLeNet은 적은 파라미터 수로 향상된 성능을 보임
인셉션 신경망 구조는 AlexNet이나 VGGNet에서 따온 고전적인 CNN 구조를 따르지만 인셉션 모듈(inception module)이라는 새로운 요소를 도입하였음
(1) 인셉션 구조에서 발전된 부분
기존 신경망 구조들은 각 층마다 합성곱층의 커널 크기와 풀링층의 배치 등의 파라미터를 결정하기 위해 다양한 시행착오가 필요했음
합성곱층의 커널 크기
- 앞서 살펴본 신경망 구조는 커널 크기가 제각각으로, 1x1, 3x3, 5x5, 큰 것은 11x11 (AlexNet)까지 있었음
- 합성곱층을 설계하다 보면 데이터셋에 맞는 커널 크기를 선택하게 됨
- 크기가 작은 커널은 이미지의 세세한 특징을 포착할 수 있고, 큰 커널은 세세한 특징을 놓치기 쉬움
풀링층의 배치
- AlexNet구조에서는 1개 또는 2개 합성곱층마다 풀링층을 배치해 특징을 다운샘플링
- VGGNet은 2, 3, 4개 합성곱층마다 풀링층을 매치했는데 신경망의 얕은 쪽에 풀링층을 더 자주 배치했음 (2개 합성곱층마다 풀링층 배치)
인셉션에서는 합성곱의 필터 크기나 풀링층의 배치를 직접 결정하는 대신 블록 전체에 똑같은 설정(인셉션 모듈)을 적용
GoogLeNet은 기존의 방식대로 층을 쌓는 대신 커널 크기가 서로 다른 합성곱층으로 구성된 인셉션 모듈을 쌓는 방식으로 신경망을 구성함
LeNet, AlexNet, VGGNet 등의 기존 방식에서는 합성곱층과 풀링층을 번갈아 쌓아 올리는 방식으로 특징 추출기를 구성함
인셉션 구조에서는 인셉션 모듈과 풀링층을 쌓아 특징 추출기를 구성함

(2) 단순 인셉션 모듈
인셉션 모듈의 구성
- 1x1 합성곱층, 3x3 합성곱층, 5x5 합성곱층, 3x3 최대풀링층
- 각 층의 출력은 연접처리(concatenation)를 통해 하나의 출력으로 합쳐져 다음 단계의 입력이 됨
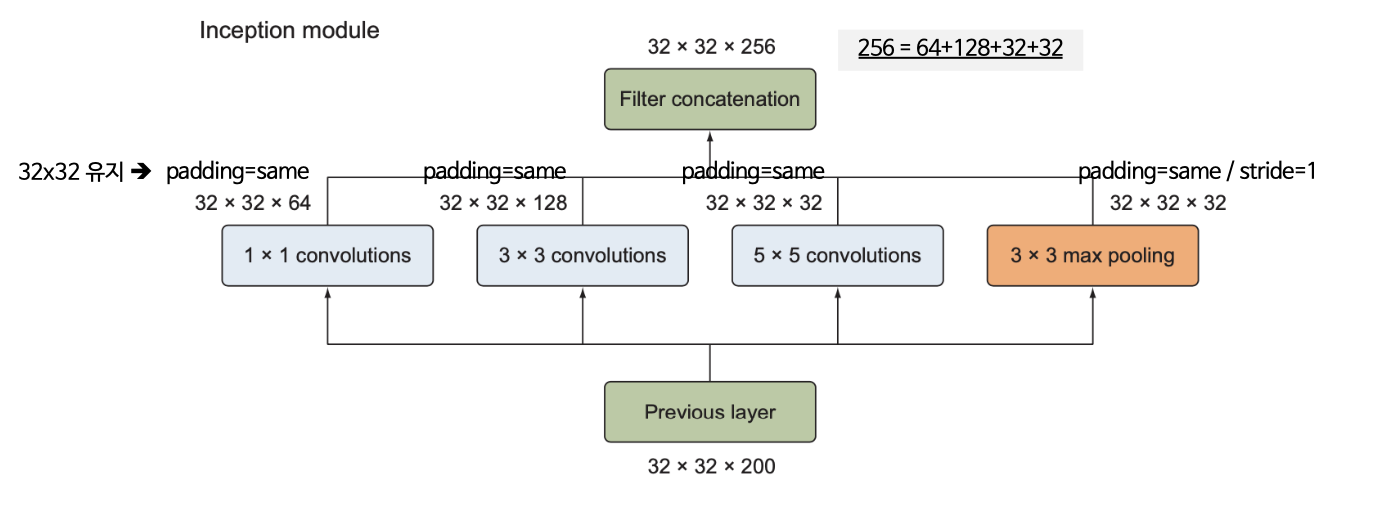
(3) 차원 축소가 적용된 인셉션 모듈
단순 인셉션 모듈은 5x5 합성곱층과 같은 크기가 큰 필터를 포함하기 때문에 계산비용이 큼
- 32x32x200 크기의 입력이 5x5 크기의 합성곱 필터 32개를 갖춘 합성곱층에 입력
- 필요한 곱셈의 수는(32x32x200)x(5x5x32) = 약 1억6300만회
이때 연산수를 줄이기 위해 차원 축소층의 도입이 필요
1) 차원 축소층 (1x1 합성곱층)
1x1 합성곱층을 도입하면 1억 6300만회의 곱셈을 약 1/10으로 줄일 수 있음
3x3 또는 5x5 처럼 크기가 큰 필터를 포함하는 합성곱층 앞에 1x1 합성곱층을 배치해서 입력의 깊이를 축소하고 필요한 연수 횟수를 줄임
연산이 줄어드는 과정
계산비용 = 1x1 합성곱층의 연산 횟수 + 5x5 합성곱층의 연산 횟수
= (32x32x200)x(1x1x16)+(32x32x16)x(5x5x32)
= 3276800 + 13107200
= 약 1630만
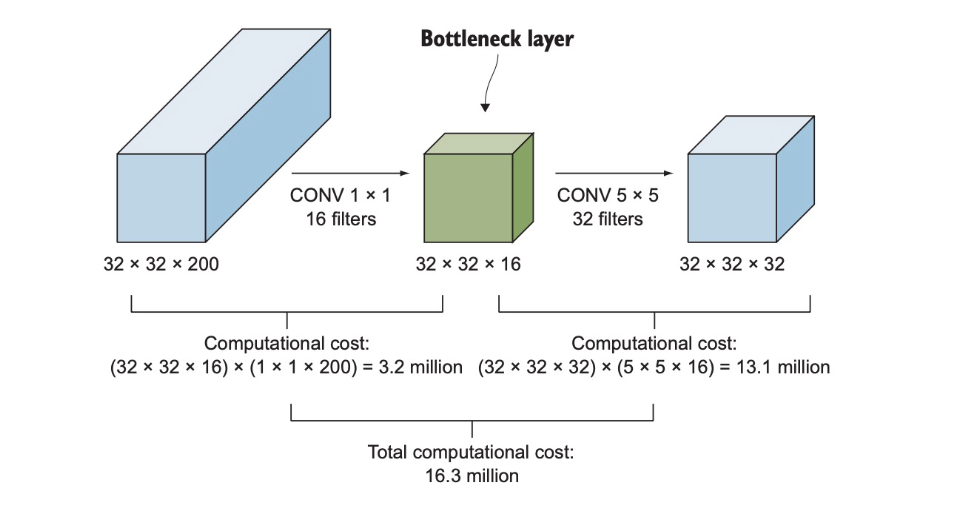
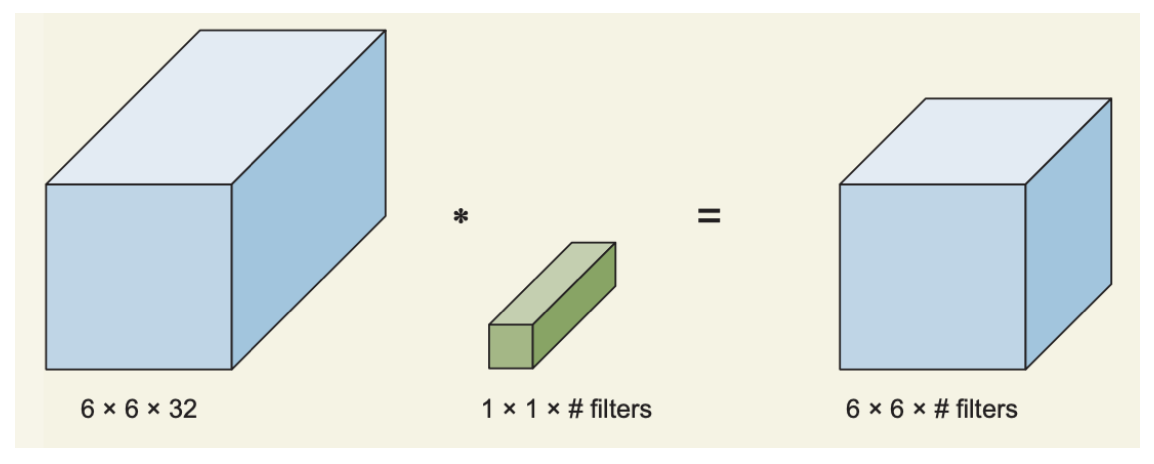
1x1 합성곱층을 이용한 차원 축소는 이 합성곱층이 이미지 크기는 그대로 유지한 채 필터수를 통해 출력의 채널수(깊이)를 자유로이 변경할수 있다는 점을 이용한 것
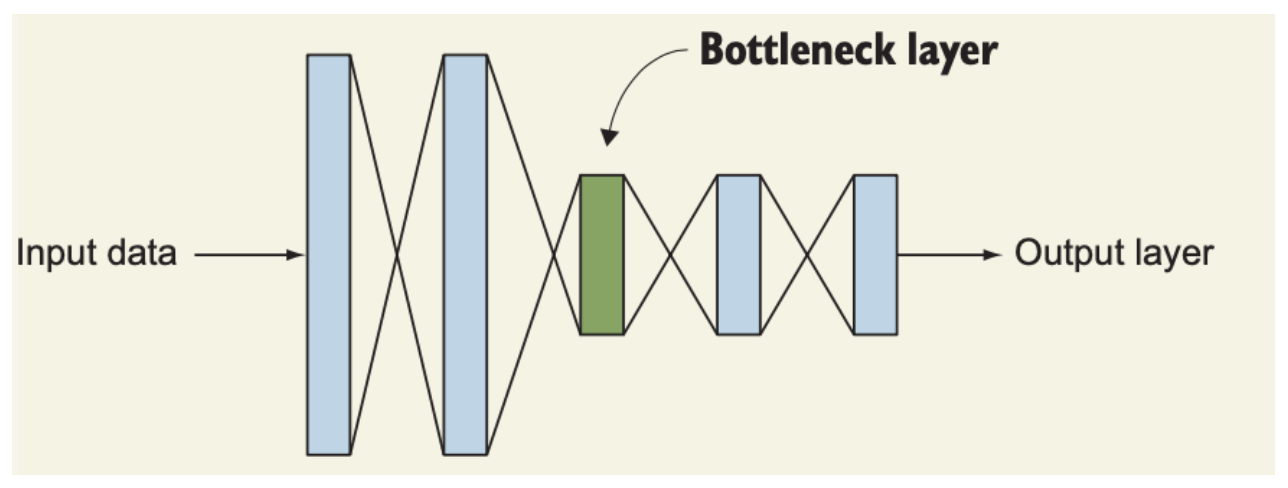
1x1 합성곱층은 병목층(bottleneck layer)라고 하는데, 신경망 구조 내에서 차원을 축소하는 이 층의 역할이 마치 병에서 가장 좁은 병목을 연상케하기 때문
2) 차원 축소가 신경망 성능에 미치는 영향
과격한 차원 축소로 신경망의 성능에 나쁜 영향을 미치지 않을까 걱정될 수 있으나, 실험 결과 적정 수준을 유지하는 차원 축소는 신경망의 성능에 영향을 미치지 않음
차원 축소가 적용된 인셉션 모듈
- 3x3, 5x5 합성곱층 앞에 각각 1x1 합성곱층을 배치
- 풀링층은 입력의 차원을 축소하지 않고, 3x3 최대풀링층 뒤에 1x1 합성곱층을 하나 배치해 풀링층의 출력에 차원 축소를 적용
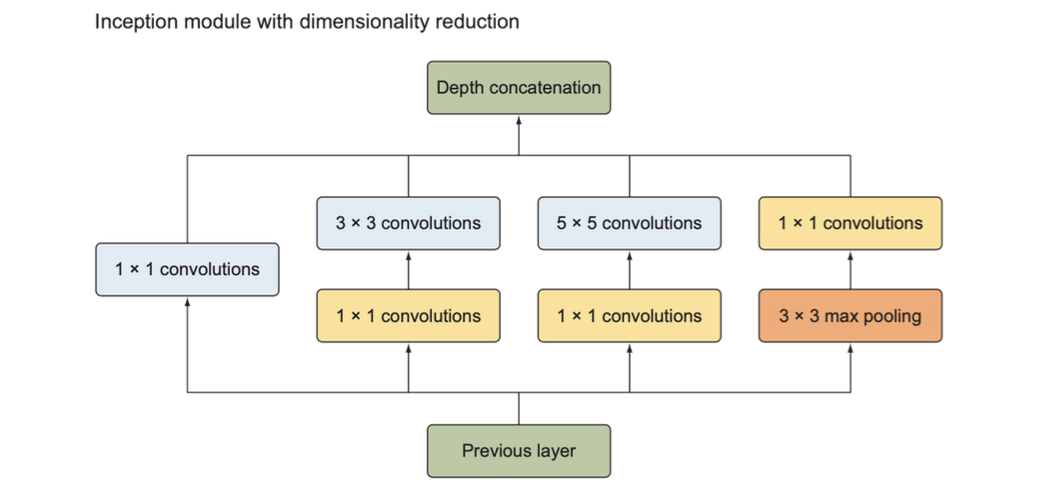
3) 인셉션 모듈 정리
합성곱층의 필터 크기나 풀링층의 위치를 따로 정하고 싶지 않다면 인셉션 모듈을 이용해서 원하는 모든 크기의 필터를 사용한 결과를 모두 연접해서 출력하면 되며, 이러한 방식은 인셉션 모듈의 단순 표현(naive representation)에 해당됨
단순 표현시 발생하는 계산 비용 문제를 해결하기 위해 3x3, 5x5 합성곱층 앞과 최대풀링층 뒤에 1x1합성곱층인 축소층을 배치할 수 있으며, 이러한 방식은 차원이 축소된 인셉션 모듈에 해당됨
(4) 인셉션 구조
차원 축소가 적용된 인셉션 모듈
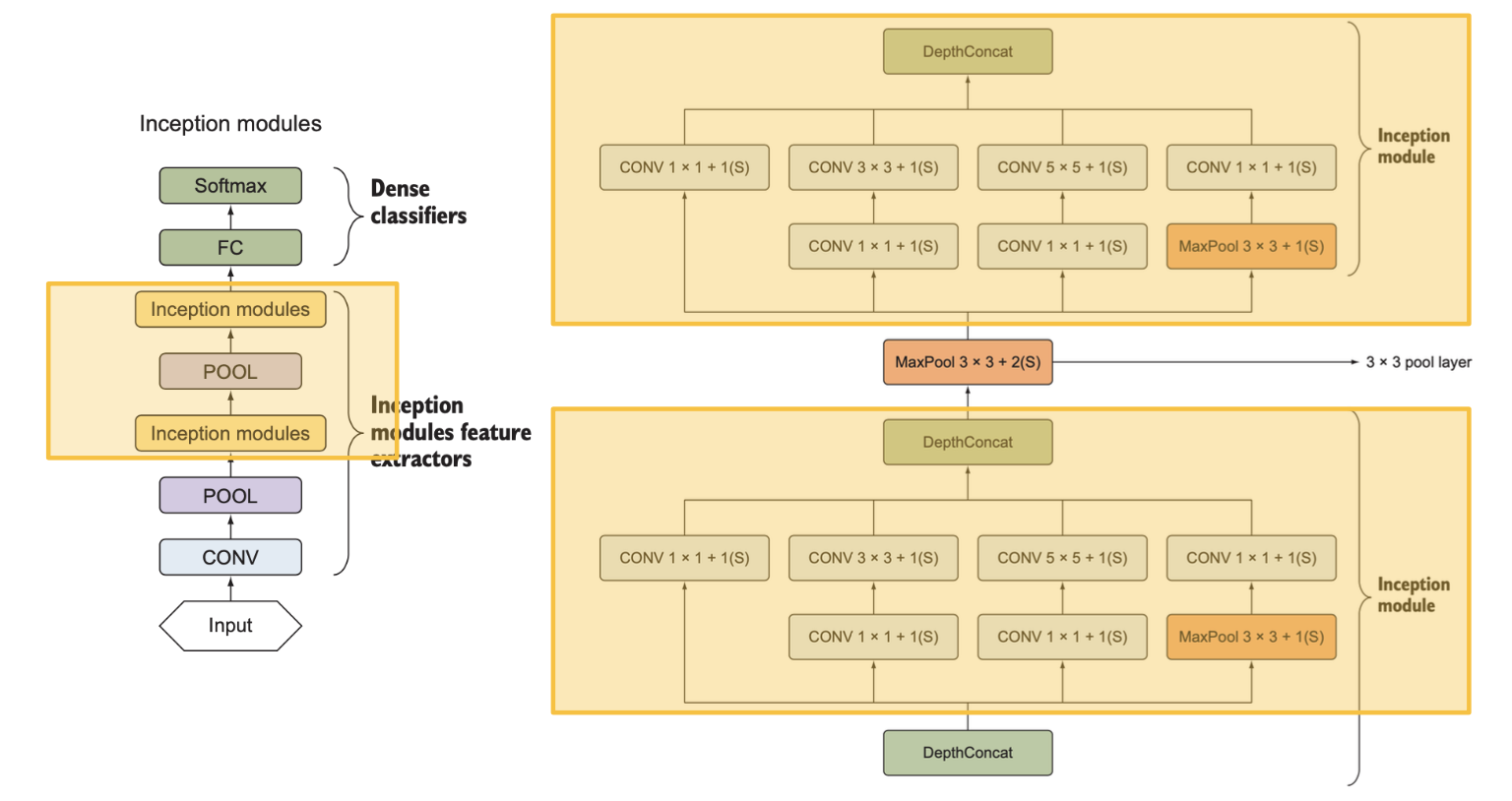
(5) GoogLeNet
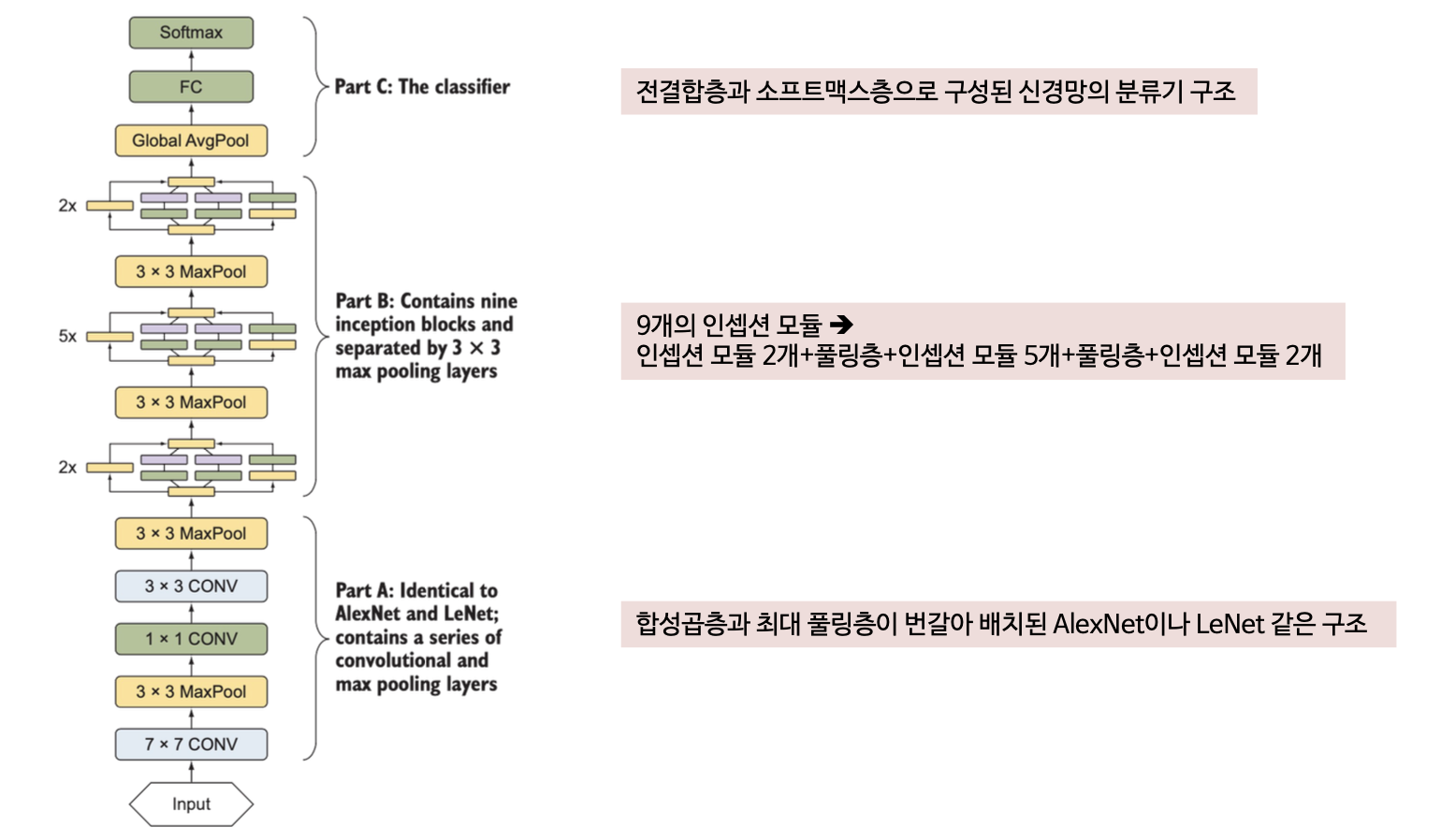
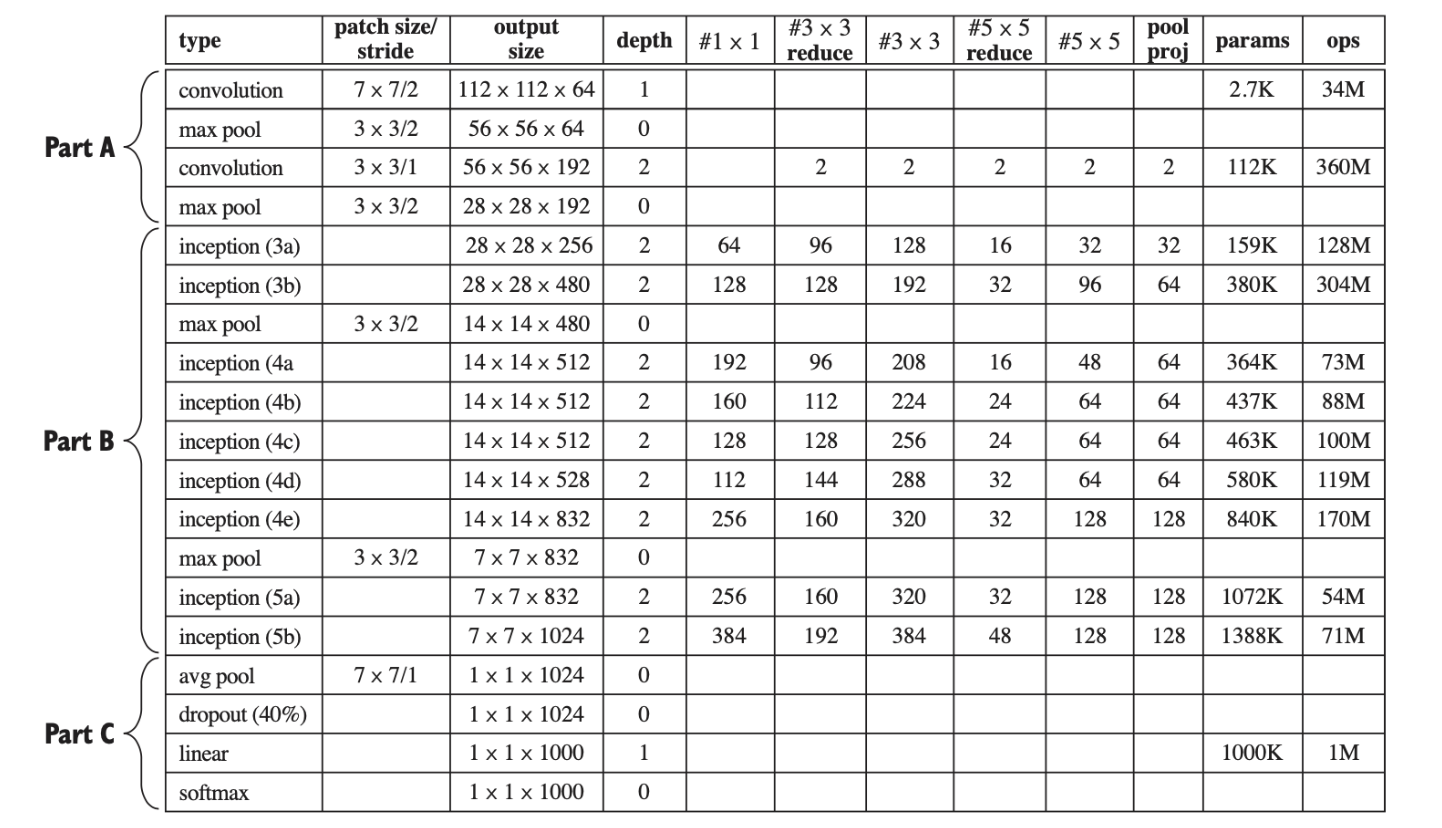
(6) 하이퍼파라미터 설정
학습률 스케줄러: 8 에포크 마다 학습률 learning rate 4%씩 감소
최적화 알고리즘: 경사하강법
모멘텀: 0.9
(7) CIFAR 데이터셋을 대상으로 한 인셉션의 성능
GoogLeNet은 2014년 ILSVRC에서 우승하였음
GoogLeNet의 top-5 오차율은 6.67%로 AlexNet이나 VGGNet 등 기존 CNN 구조보다 훨씬 뛰어난 것은 물론이고 사람에 필적할만한 성능을 보였음
6. ResNet (Residual Neural Network)
잔차 신경망(ResNet)은 2015년에 마이크로소프트 리서치 팀에서 제안한 신경망 구조
ResNet에는 잔차 모듈(residual module)과 스킵 연결(skip connection)이라는 새로운 구조가 사용되었으며, 은닉층에도 강한 배치 정규화가 적용되었음
ResNet은 2015년에 ILSVRC에서 top-5 오차율 3.57%을 기록하며 가장 좋은 성능을 기록함
배치 정규화가 강하게 적용된 덕분에 파라미터가 있는 층이 50층, 101층, 152층이나 되는 깊은 신경망(ResNet50, ResNet101, ResNet152)의 복잡도를 훨씬 층수가 적은 VGGNet(19층)보다 낮출 수 있음
신경망이 지나치게 깊어지면 과적합이 발생하기 쉬움
ResNet은 배치정규화를 통해 과적합 문제를 해결하였음
(1) ResNet에서 발전된 부분
LeNet → AlexNet → VGGNet → GoogeLeNet 신경망 구조의 발전을 통해 신경망의 층수가 많을수록 이미지에서 더 좋은 특징을 추출할 수 있다는 것을 발견함
일반적으로 신경망의 층수가 많을수록 신경망 모델의 표현력이 좋아지며, 이는 단순한 모서리(앞쪽층)에서 부터 복잡한 패턴(뒤쪽층)에 이르기까지 다양한 추상화 수준의 특징을 학습할 수 있기 때문임
VGG19(19층)와 GoogLeNet(22층) 구조보다 신경망 층수를 늘리기 위해서는 과적합 문제와 기울기 소실 문제를 해결해야 함
과적합 문제는 드롭아웃, L2규제화, 배치정규화를 통해 해결 가능
기울기 소실 문제는 ResNet 구조가 제안한 스킵 연결을 통해 해결 가능
ResNet 연구진은 기울기 소실문제 해결을 위해 스킵 연결을 제안함
스킵 연결이란 뒤쪽 층의 기울기를 앞쪽 층에 직접 전달하는 별도의 경로를 추가하는 것으로 앞쪽 층의 정보가 뒤쪽 층에 전달하는 것을 의미함
스킵 연결은 항등함수를 학습할 수 있어 층이 쌓여도 앞쪽 층보다 성능이 하락하지 않는 역할을 수행함
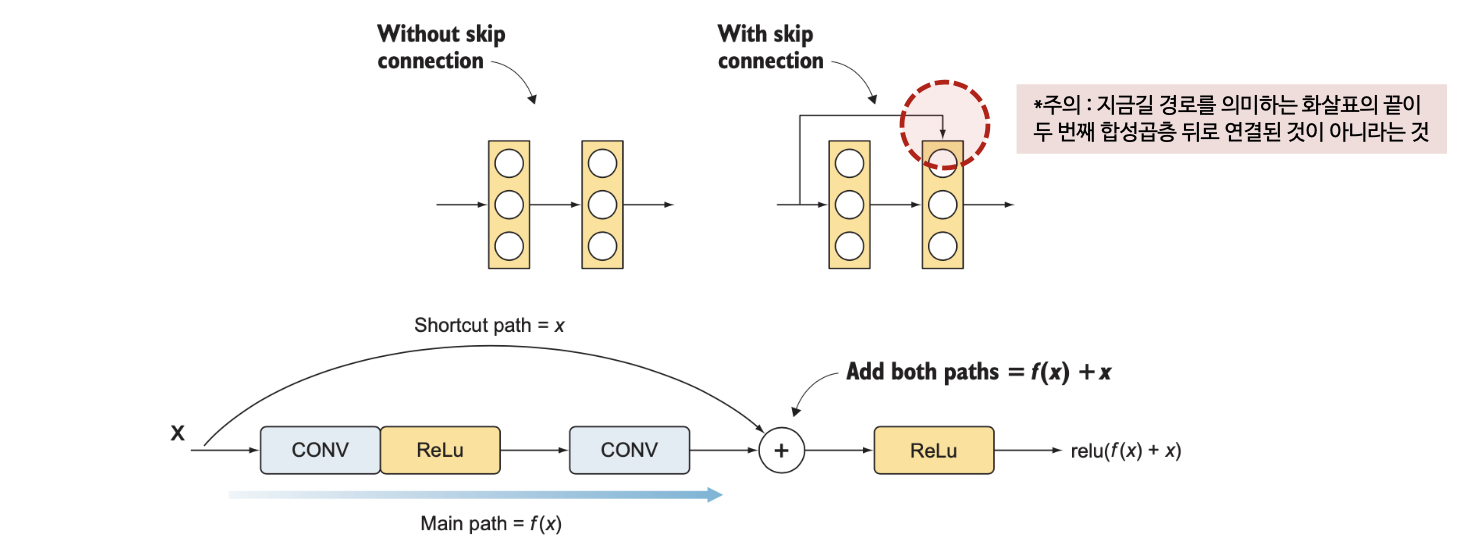
합성곱층에 스킵 연결을 추가한 구조를 잔차 블록(residual block)이라고 함
인셉션과 마찬가지로 ResNet 구조도 여러 개의 잔차 블록이 늘어선 형태로 구성됨
- 특징추출기 : ResNet의 특징추출기 부분은 합성곱층과 풀링층으로 시작해서 그 뒤로 잔차블록이 1개 이상 이어지는 구조로, ResNet은 원하는만큼 잔차 블록을 추가해서 신경망의 층수를 늘릴 수 있음
- 분류기 : 분류기 부분은 다른 신경망과 마찬가지로 전결합층과 소프트맥스 함수로 구성됨
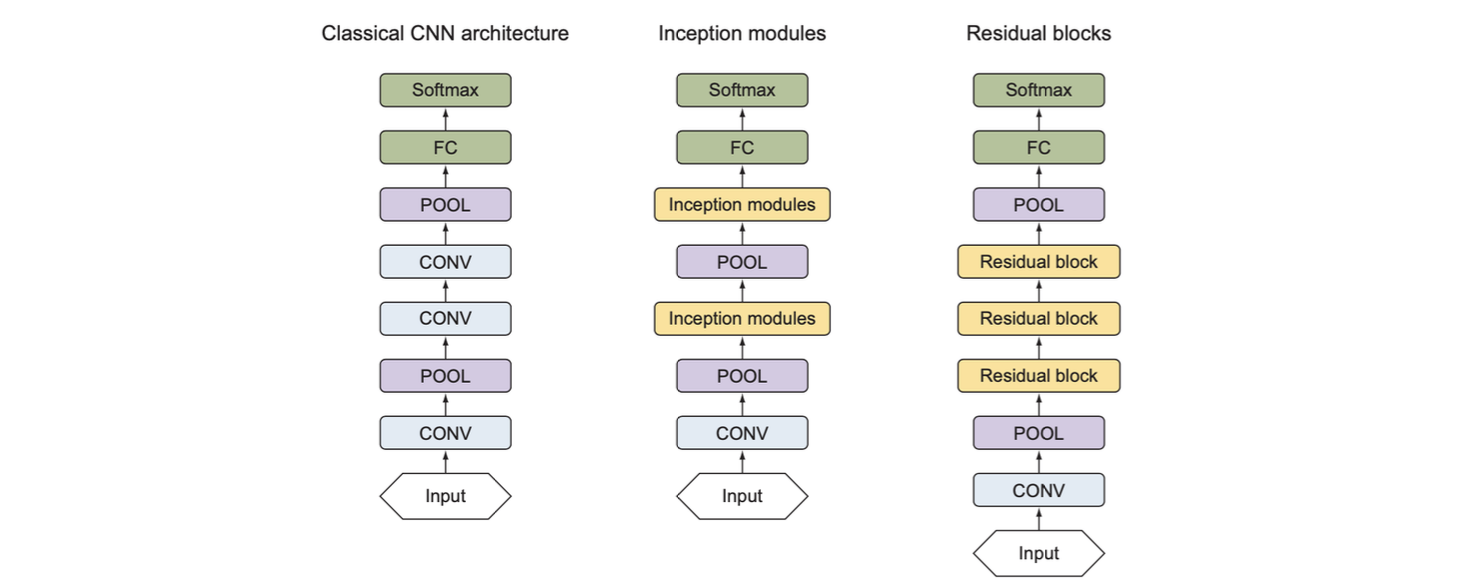
(2) 잔차 블록
잔차 블록(residual block)은 다음 2개의 경로로 나뉨
- 지름길 경로 : 입력을 주경로의 ReLU 입력 전으로 전달함
- 주경로 : 일련의 합성곱 연산 및 활성화 함수로, 주경로는 ReLU 활성화 함수를 사용하는 3개의 합성곱층으로 구성됨. 과적합 방지와 학습 속도 향상을 위해 각 합성곱층마다 배치 정규화를 적용함. 결과적으로 주 경로의 구조는 [CONV=>BN=>ReLU]x3 와 같음
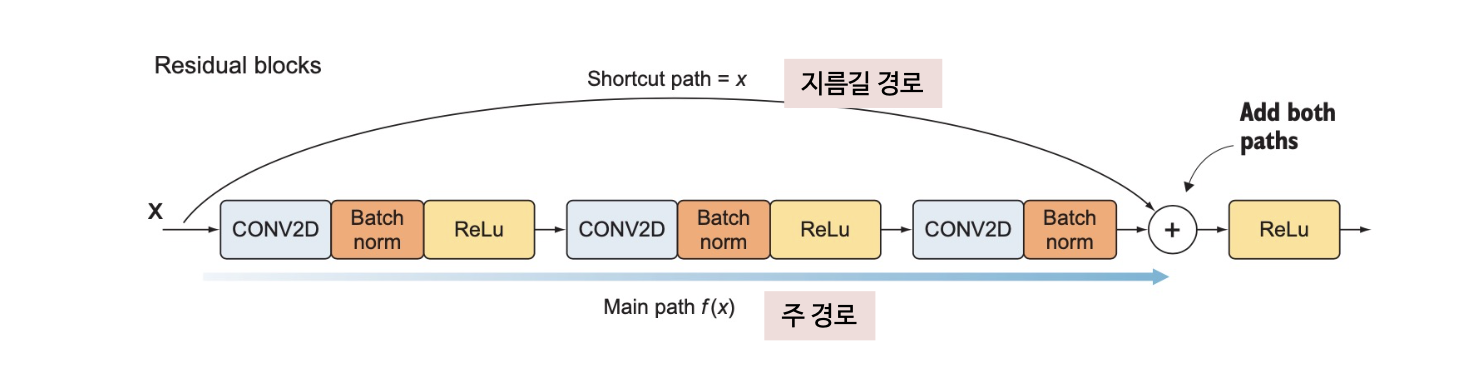
지름길 경로의 값은 잔차 블록 마지막 합성곱층의 활성화 함수 바로 앞에서 주경로의 값과 합하여 이 값을 ReLU 함수에 통과시킴
잔차 블록에는 풀링층이 없음
인셉션 구조와 비슷하게 1x1 합성곱층을 사용하여 다운샘플링을 적용
- 잔차블록 처음에 1x1 합성곱층을 배치하고, 출력에는 3x3 합성곱층과 1x1 합성곱층을 하나씩 배치해서 두번에 걸쳐 차원을 축소함. 이구조는 여러 층에 걸쳐 입출력의 차원을 제어할 수 있다는 것이 장점
- 차원축소가 적용된 블록을 병목잔차블록(bottleneck residual block)이라고 함
주 경로와 지름길 경로로 전달되는 정보의 차원이 동일해야 연산(행렬덧셈)이 가능
- 주경로에 차원축소층을 적용하여 정보의 차원을 축소했다면, 지름길 경로에도 병목층(1x1합성곱층+배치정규화)을 적용하여 정보의 차원을 축소해야 함
- 이러한 구조를 축소 지름길 경로(reduce shortcut)라고 함
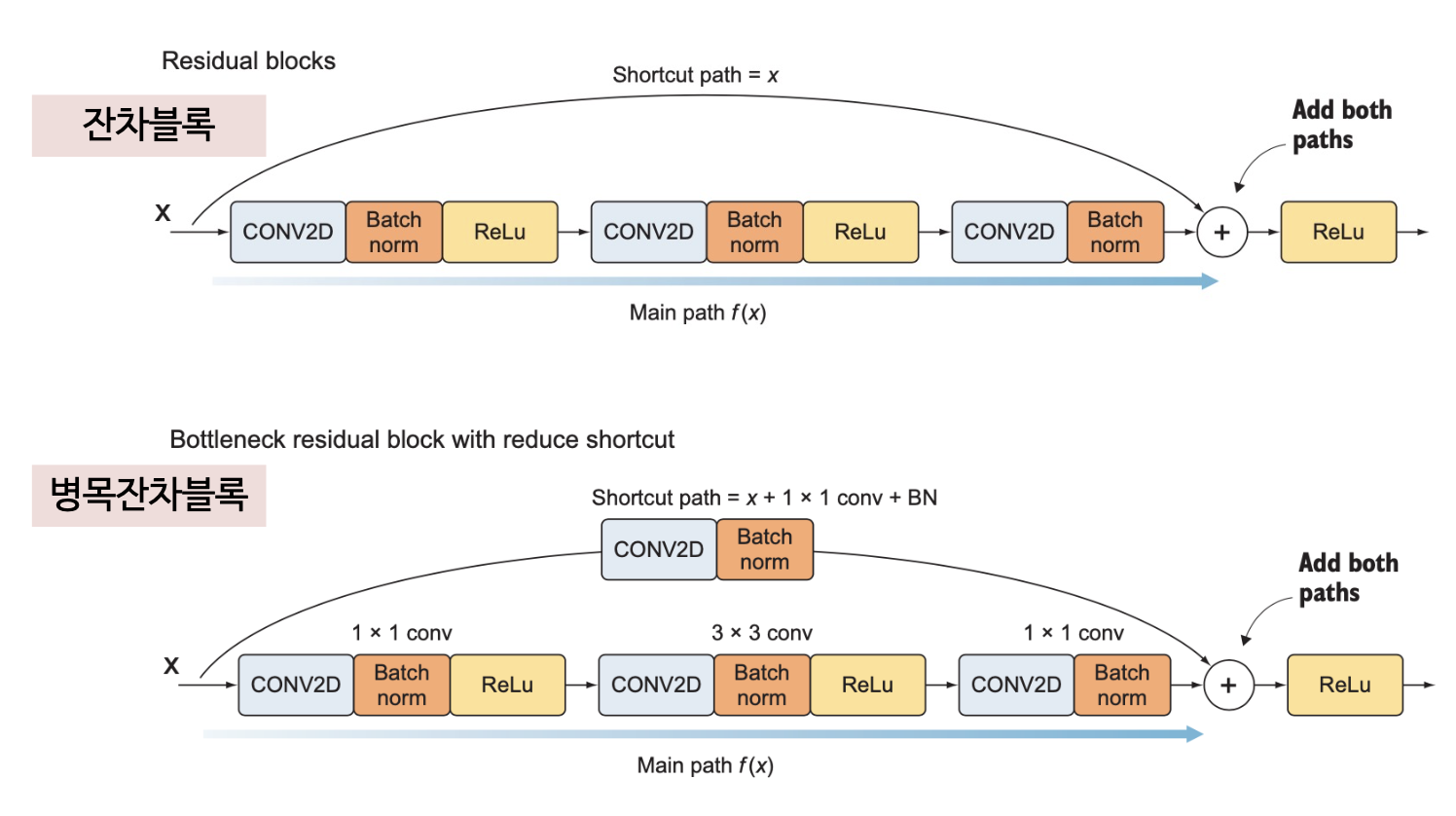
잔차 블록에는 지름길 경로와 주경로가 있음
주경로는 3개의 합성곱층에 각각 배치정규화가 적용됨
- 1x1 합성곱층
- 3x3 합성곱층
- 1x1 합성곱층
지름길 경로를 구현하는 1x1합성곱층 방법은 두가지
- 일반 지름길 경로 : 주경로와입력을더하는일반적인지름길경로
- 축소 지름길 경로 : 주경로와입력을더하는지점이전에합성곱층이하나배치된 지름길 경로
(3) ResNet 구현
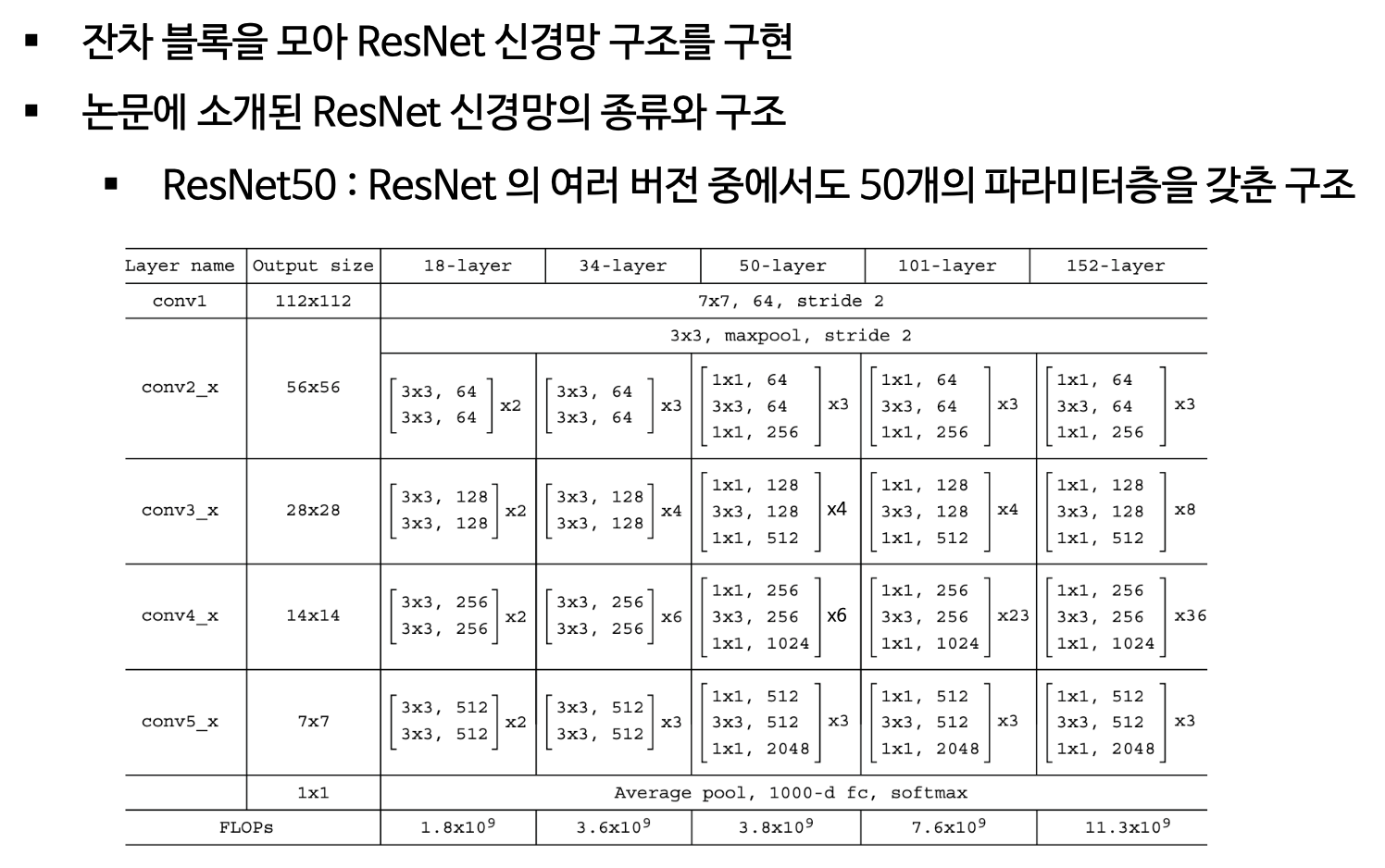
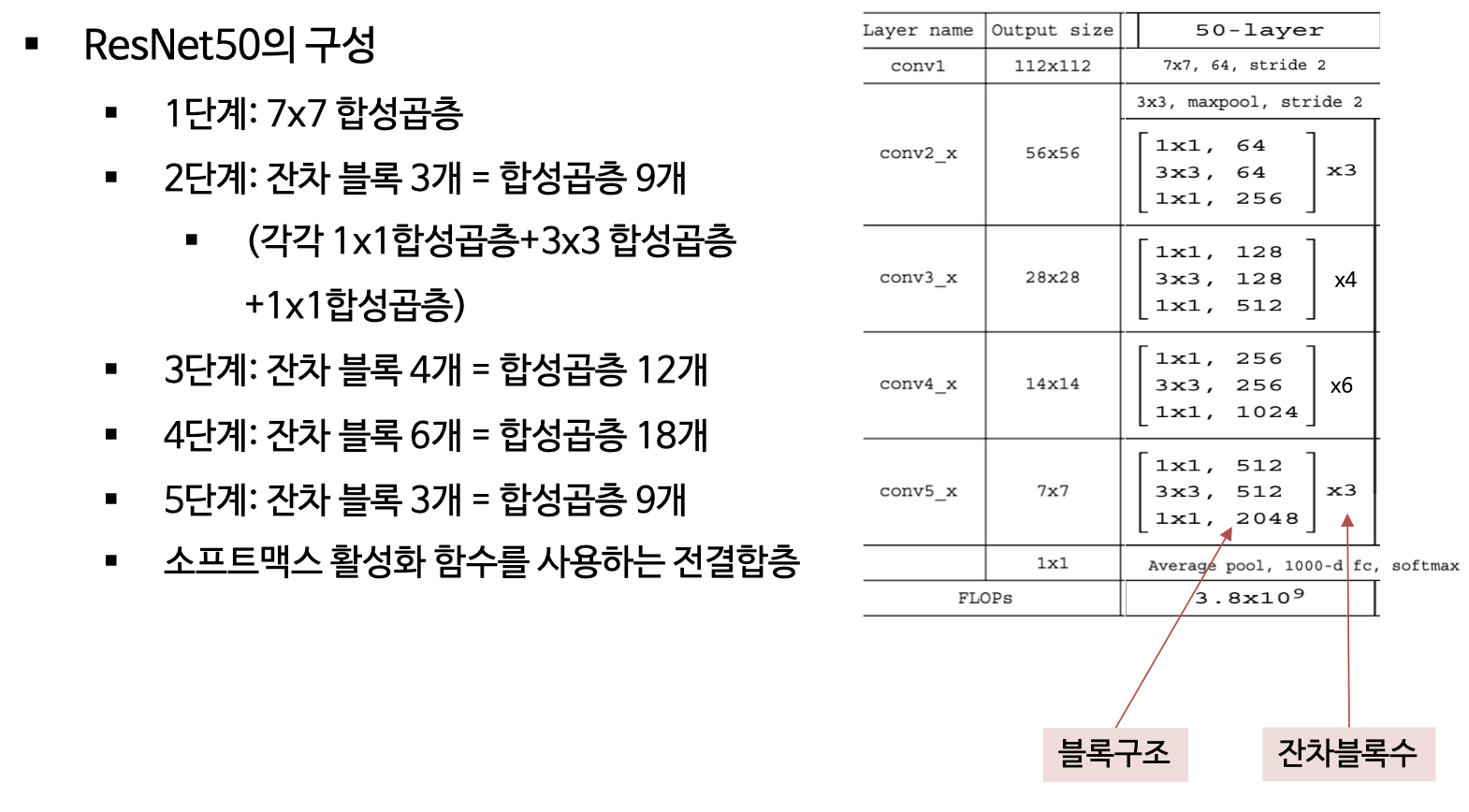
(4) 하이퍼파라미터 설정
미니배치 경사하강법
모멘텀 : 0.9
학습률 초기값 : 0.1 (검증오차 감소 없을시 학습률 1/10 감소)
가중치 감소율 : 0.0001
L2규제화 함께 사용 (단, 아래 구현코드에서는 생략)
(5) ImageNet 데이터셋을 대상으로 한 ResNet의 성능
[2015년 ILSVRC]
- ResNet-512 : top-5 오차율 4.49% 달성
- 앙상블 모델 : top-5 오차율 3.57% 달성 (우승)
- GoogLeNet : top-5 오차율 6.67%
7. 마치며
기본적인 합성곱 신경망 구조는 서로 다른 설정을 가진 합성곱층과 풀링층을 번갈아가며 배치하는 방식으로 구성된다.
LeNet은 5개의 파라미터층(3개는 합성곱층, 2개는 전결합층이며, 첫번째와 두번째 합성곱층 뒤에는 풀링층이 배치)으로 구성된다.
AlexNet은 LeNet보다 많은 8개의 파라미터층(5개는 합성곱층, 3개는 전결합층)을 갖는다.
VGGNet은 전체 신경망에서 동일한 하이퍼파라미터 설정을 사용하는 방식으로 합성곱층 및 풀링층의 하이퍼파라미터 설정 문제의 해결을 시도했다.
인셉션은 VGGNet과는 다른 방식으로 하이퍼파라미터 설정 문제를 해결하려 했다. 특정 필터 또는 풀링 크기를 지정하는 대신 다양한 필터 크기와 풀링 크기를 한꺼번에 사용했다.
ResNet은 인셉션과 비슷한 접근 방식으로 잔차 블록을 도입했다. 전체 신경망은 이 잔차 블록으로 구성된다. 신경망의 층수가 일정 이상 어나면 기울기 소실 문제로 학습이 잘되지 않는데, 신경망의 서로 떨어진 층을 이어주는 스킵 연결 도입을 통해 기울기를 전달했다. 이런 방법으로 수백 층에 이르는 거대한 신경망의 학습을 가능케 하는 돌파구를 열었다.
'Computer Science > Deep Learning' 카테고리의 다른 글
| 전이학습(Transfer Learning) (2) (1) | 2024.06.09 |
|---|---|
| 전이학습(Transfer Learning) (1) (0) | 2024.06.09 |
| 고급 합성곱 신경망 ① (0) | 2024.04.17 |
| 하이퍼파라미터 튜닝 ② [CIFAR-10] (0) | 2024.04.17 |
| 하이퍼파라미터 튜닝 ① (1) | 2024.04.17 |




